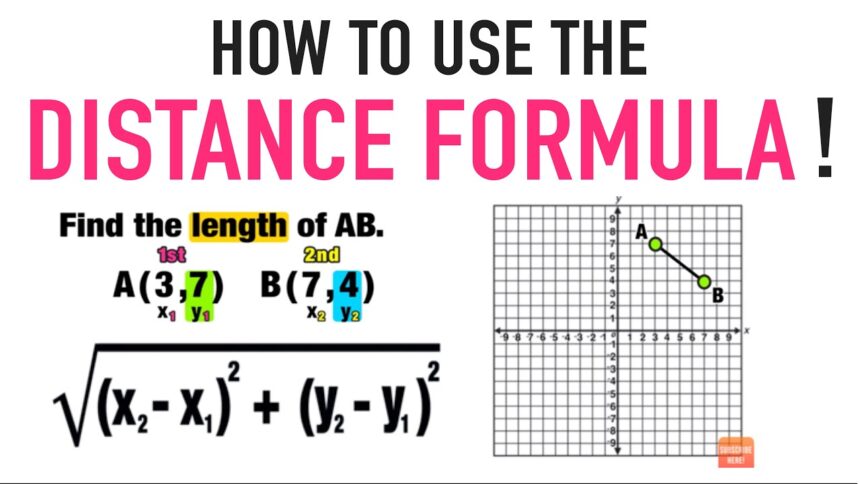
Distance is a measurement of length, either numerically or qualitatively. It can be a physical length or an estimate based on other factors. In this article, you will learn how to find the distance between two points, two parallel lines, or two points and lines in Cartesian coordinates. The formula is simple and straightforward.
Distance between two points
The distance formula is a useful tool for calculating distance between two points. It is a mathematical formula that always holds true. In fact, it can even be used to plot two points to find their hypotenuse, which represents the distance between them. The following example will show you how to use it.
To find the distance between two points, write down the x and y coordinates of the points you want to compare. Then, take the difference between the two x and y coordinates and multiply that by two. Then, take the square root of the difference. You should now have the distance between the two points. This formula is very useful for measuring distance between points that are far apart. But be sure to follow the order of operations!
The distance formula between two points can also be used to determine distances between diagonal line segments of a coordinate grid. As a result, it can be related to the Pythagorean Theorem. However, unlike the Pythagorean Theorem, this formula cannot be used to determine the distance between two points based on a single line segment.
Distance between two parallel lines
The distance formula between two parallel lines is an equation involving two points. The slopes of the lines must be equal and they must have a common interception point. For example, a line from point A to point B intersects the x-axis at point A (-c 1 /m). The distance between the two lines is equal to the length of the perpendicular to line A.
In mathematics, lines are formed when two points are placed on the same plane. Lines join at their lowest distance. This distance is called the perpendicular distance. There are many types of lines: parallel, skewed, intersecting, and perpendicular. This article will show you how to calculate the distance between two straight, parallel, or skewed lines.
The distance between two parallel lines is equal to the slope of their perpendicular lines. Therefore, the distance between two parallel lines is the shortest distance between the two points.
Distance between two parallel lines in Cartesian coordinates
The distance between two parallel lines can be calculated using the distance formula. To calculate this distance, you will need the slope values of both lines. Once you have these values, you will substitute them into the slope-intercept equation to get the value of y. In the distance formula, the value of y is the distance between the two lines.
If the lines are parallel, then they are coplanar. The distance between these two lines is the length of the perpendicular between them. If they intersect, the distance is zero. If the distance is greater than zero, then they are not parallel. If you are unsure, you can use the distance formula to determine the distance between two parallel lines.
The shortest distance between two parallel lines is the length of one perpendicular segment. A perpendicular segment can be any length as long as it is perpendicular to the two parallel lines. This method is useful to calculate the distance between two lines. In Cartesian coordinates, this distance is known as the distance between two parallel lines.
Lambert’s formula
Lambert’s formula for distance can be used to find the distance between two points. It is derived from the Pythagorean theorem and is based on the idea of right triangles. The two sides of a right triangle are called a and b, while the hypotenuse is called c. The formula can be used to find distances between two points as well as calculate the midpoint between two points.
Compared to the haversine formula, Lambert’s formula is more accurate and can be used to calculate distances over thousands of kilometers. It works by using the equatorial radius of an ellipsoid and the central angle in radians of latitude and longitude. It also takes into account the flattening of the Earth’s surface.
Lambert’s formula for distance can also be applied to lines of different orientation. It works for horizontal and vertical lines, as the length of a horizontal line is equal to the difference between the x and y-coordinates of the other point. To find the length of a line, you can simply subtract the two coordinates and use the formula to calculate the distance.
Pythagorean theorem
The Pythagorean Theorem is a fundamental tool for understanding distance between two points. It can be used to determine the length of the hypotenuse of a right triangle. It is the distance between two points divided by two. The formula for determining distance can be found by calculating the formula: Distance2 = (x2-x1)2 + (y2-y2)2
This formula is also useful for calculating the slope of a hill. In addition to calculating distances, Pythagoras’s theorem can be used to calculate the diagonal of a square and the side lengths of a right triangle.
The Pythagorean Theorem is a fundamental math concept that is used in many fields. It is used to determine the distance between two points in a coordinate plane and to solve many real-world problems. You can use it to find the length of a right triangle, find the missing coordinate of a point, or find the midpoint of a line segment.
Distance squared
The distance squared formula can be used to calculate the distance between two points. To calculate the distance between two points in two dimensions, you must first know the values of x and y. For three-dimensional distances, you must know the values of x, y, and z. The distance formula is also useful in finding the length of the hypotenuse between two points.
The distance formula is derived from the Pythagorean Theorem. You can use it to find the length of the hypotenuse of a right triangle. Then, you can multiply the result by the square root of the difference between the two points. Once you’ve done that, you can calculate the distance between two points.
You can also use the distance squared formula to find the minimum distance between two points. The formula works the same for positive and negative distances. The area of a square grows as the size of the square increases.
Distance squared equal to 9 plus 16
If you want to find out how long a distance is, use the formula distance squared equal to nine plus 16. This is a common formula that can be used to find the distance between two points. To use this formula, write down the x and y coordinates of each point. Next, add up the x and y differences. Then, take the square root of the remainder to find the distance.
Distance squared equal to 25
Distance squared equal to 25 is a formula for calculating distance. The formula is derived from the Pythagorean theorem. The formula states that a change in x or y equals the distance squared. For example, a change of 25 feet is equal to a change of 25 meters.