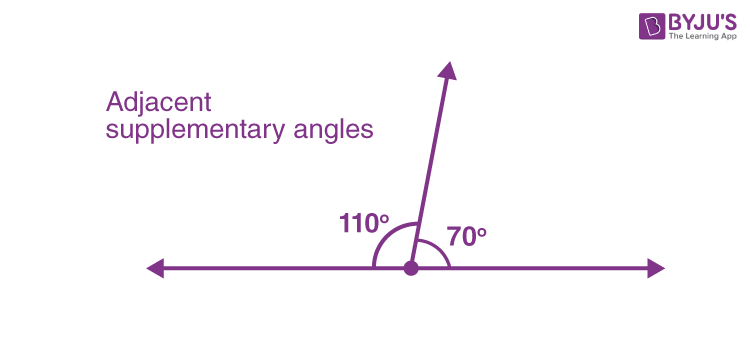
Supplementary angles are angles that are adjacent to each other and form a straight line. These angles are also known as complementary angles. In geometry, they are commonly used to define polygons. There are two types of supplementary angles: those with adjacent vertex, and those without. In general, they are similar to one another, but they differ from one another in one important way.
Complementary angles are two angles with a sum of 90 degrees
Complementary angles are two angles whose sum equals ninety degrees. They are also known as ‘right angles’ because they share the same side and rays. To determine whether two angles are complementary, first identify their measures. For example, 31 degrees and 59 degrees are complementary angles.
Complementary angles do not need to be adjacent, but their sum must be at least 90 degrees. Their names come from Latin “completum,” which means “complete.” This is why we often think of the right angle as a “complete angle,” despite the fact that it does not have an ‘i’.
Complementary angles are not always adjacent. Some are “non-adjacent” and some are “adjacent.” In general, complementary angles have the same vertex and arm. They also share the same right angle. But there are certain exceptions to this rule.
Complementary angles are angles with the same measure. They are the same shape but differ in their sums. Complementary angles are a good example of this rule in math. In a simple example, an angle with a 90-degree sum is an acute angle.
Complementary angles are two angles that add up to 180 degrees. The greater angle is three times greater than the smaller one, and the smaller one is two times greater. This gives us a 90 degree-180 degree triangle. Similarly, an angle of 100 degrees and 80 degrees is a supplementary angle.
Supplementary angles are two angles with a sum of 180 degrees
Supplementary angles are two angles that add up to 180 degrees and form a straight line. The sum of these two angles is equal to the sum of other pairs of supplementary angles. In mathematics, supplementary angles are often used to measure the length of a line.
The two angles do not need to be adjacent. For example, angles 3 and 4 are supplementary because their measurements are the same and their sum is 180 degrees. Angles X and Y are supplementary if their sum is greater than 24 degrees. The sum is called the “supplement”.
Two supplementary angles form the right angle and the supplementary angle. These two angles are equal, but differ in size and shape. In addition, they have opposite properties. In addition, supplementary angles can be a pair of angles that have the same length. In geometry, this can happen in many ways.
Supplementary angles are angles that are adjacent but not identical to each other. These two angles form a straight line when put together. Those angles can be either adjacent or non-adjacent, but they must add up to 180 degrees. In addition to the two types of supplementary angles, there are auxiliary angles and supplementary angles.
Supplementary angles are angles that have the same length and share a common vertex or arm. They add up to 180 degrees and are considered complementary. If you have a similar right angle, they are complementary. If one is obtuse, the other is a right angle.
Complementary angles are angles that have the same length and share the same angle. These angles are often called corner angles.
They form a straight angle
Supplementary angles are angles on the same side of a line that are congruent to each other. When they add up to 180 degrees, they form a straight angle. The most common application of supplementary angles is at crossroads. They can also be separated from one another.
There are three different types of supplementary angles. Each supplementary angle has its own special characteristics. One type of supplementary angle is a straight angle, while the other is a curved angle. In general, supplementary angles form a straight angle. They may be obtuse or acute, but must sum up to 180 degrees in order to be considered supplementary.
Subsidiary angles are formed by taking the sum of two other angles. The two angles that make up a supplementary angle are called complementary angles. They measure 103 degrees in each direction and add up to 180 degrees when added together. They are sometimes referred to as “right angles.”
A straight angle is a line segment formed from two perpendicular segments. The angle forming a right triangle is a complementary angle. Its complementary angles are supplementary. In addition, a straight angle is formed from two angles that are 90 degrees apart. If two supplementary angles are congruent, they form a right triangle.
If two supplementary angles add up to 180 degrees, they form a straight line. They must share a vertex and share a side. They must also have non-common sides. Lastly, they must be the same size.
They are adjacent
In mathematics, adjacent angles are angles that share a common vertex or side. These angles are considered adjacent because they are next to each other, not because they overlap. The most simple way to identify adjacent angles is by looking at their common vertex. But there are other ways to distinguish adjacent angles. Here are three ways.
The first type is a pair of parallel angles. These angles have the same vertex and the same side, and must sum up to 180 degrees to be considered adjacent. The second type is a pair of angles that do not intersect. These angles are not necessarily adjacent. They can be opposite or supplementary to each other, but they must sum to 180 degrees.
Another type of supplementary angle is a pair of 90-degree angles that are adjacent. These angles are often called “linear pairs” and have a common vertex. These angles can be either a triangle or straight line. Whether or not they are adjacent, they form a line.
A supplementary angle is adjacent to an interior angle, and is not necessarily congruent. It’s not always necessary to have them coincide with each other. It’s also possible to have a supplementary angle at the intersection of two parallel lines. These are considered adjacent if they are adjacent and are parallel.
Another way to identify supplementary angles is by looking at their measures. When two angles have the same measure and add up to 180deg, they are considered supplementary.
They are not joined with each other
In geometry, complementary angles are those that are not joined together. There are two types: adjacent complementary angles and non-adjacent complementary angles. Complementary angles share a vertex, arm, and right angle, but are not joined together. In some situations, they can be congruent.
In mathematics, supplementary angles are used to create right angles. If two angles are joined together, they form a 90-degree right angle. Otherwise, they form a straight line. When complementary angles are joined together, they are called adjacent supplementary angles. This is because they share a common line segment or vertex. The same holds true for supplementary angles that are not joined with each other.
The two angles ABC and PQR are not adjacent. They have the same arm, but are not joined together. Therefore, they are supplementary angles. The supplementary angles of these two angles sum to 180deg. However, they do not have to be joined with each other.
Besides adjacent angles, supplementary angles can also be contiguous. When two supplementary angles are adjacent, they will have the same measure and add up to a right angle. A right angle and an acute angle are complementary. The other way to see this is by using a diagram, in which the supplementary angles form an equilateral triangle.
An angle that is adjacent to another has a common arm and vertex. The two supplementary angles that are not adjacent to each other are called non-adjacent supplementary angles.